Формулы математической статистики. Случайная величина. Среднее, поле рассеяния, дисперсия, среднеквадратичное отклонение. Скользящее среднее, полосы Боллинджера.

Математическая статистика изучает общие вопросы анализа массовых количественных данных. При этом, количественные значения рассматриваются как случайные величины, т.е. значение величины определяется множеством факторов случайного характера. Хорошим примером случайной величины служат показатели финансовых рынков: цены акций на бирже, курсы валют на рынке Forex.

Обозначения:

• X - значение случайной величины.
• N - количество значений случайной величины

1. Математическое ожидание (expected value) случайной величины

В обычной жизни известно, как среднее арифметическое.
  
Несмотря на простоту, среднее арифметическое играет большую роль в математической статистике при анализе последовательностей случайных величин. Например, в техническом анализе рынка Форекс и других финансовых рынков большое значение имеет скользящее среднее.

2. Скользящее среднее (MA - Moving average)

Скользящее среднее служит основой для многих графических индикаторов, отражающих информацию о состоянии рынка Форекс или других финансовых рынков.

Скользящее среднее получает конкретное название в зависимости от количества наблюдений, принятого для его построения. Например: МА-10 - это скользящее среднее, построенное на информации о котировках валютных пар Форекс за предшествующие 10 периодов. Трейдеры используют разные типы скользящих средних: простое, взвешенное, экспоненциальное.

3. Поле рассеяния (range - диапазон) случайной величины

R = Xmax - Xmin

4. Середина поля рассеяния (midrange)

MR = Xmin + R/2 = (Xmax + Xmin)/2.

5. Дисперсия (variance) случайной величины. Одно из важнейших понятий математической статистики.

    

6. Cтандартное отклонение (standard deviation). Одно из важнейших понятий математической статистики.

Другое название - среднеквадратичное отклонение.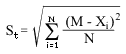

    

7. Оценка S

Для малых N иногда используют формулу: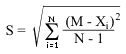

    

8. Полосы Боллинджера (Bollinger bands)

Полосы Боллинджера служат примером использования одной из характеристик математической статистики, стандартного отклонения, при техническом анализе финансовых рынков. Они строятся следующим образом. Например, анализируются котировки Форекс. Одним из методов строится линия скользящего среднего цены.

Верхняя и нижняя границы полос Боллинджера проводятся на расстояниях, равных определенному числу стандартных отклонений, обычно — 2. Поскольку величина стандартного отклонения зависит от изменчивости цены, полосы меняют свою ширину: она увеличивается, когда рынок неустойчив, и уменьшается в более стабильные периоды.

9. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача -- пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.