Теорема Пифагора, доказательство и пременение.

Обозначения:
A, B, C — углы треугольника, причем, B = 90°,
a, b, c — противолежащие стороны,
R — радиус описанной окружности,
r — радиус вписанной окружности,
p — полупериметр, (a + b + c) / 2,
S — площадь треугольника.

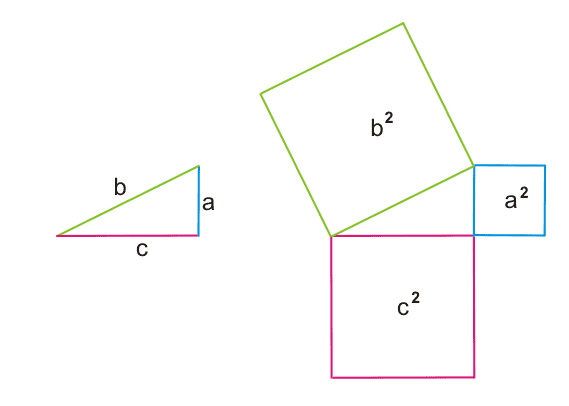
Теорема Пифагора

b2 = a2 + c2

На приведенном ниже рисунке показана геометрическая интерпретация теоремы Пифагора.

Приведем несколько простых доказательств теоремы.

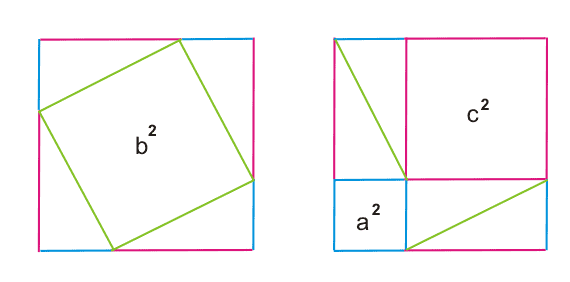
1. Самое простое доказательство теоремы Пифагора.

Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a + c.

В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.

В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.

Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.

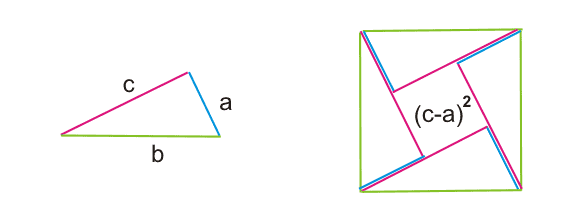
2. Доказательство индийского математика Бхаскари.

Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна b, на квадрат наложены 4 исходных треугольника с катетами a и c, как показано на рисунке.

Сторона маленького квадрата, получившегося в центре, равна c - a, тогда:
b2 = 4*a*c/2 + (c-a)2 =
   = 2*a*c + c2 - 2*a*c + a2 =
   = a2 + c2

См. также:

• Формулы треугольника
• Тригонометрические функции и обратные тригонометрические функции

3. Алгебраическое доказательство теоремы Пифагора (доказательство Мёльманна).

Площадь прямоугольного треугольника
S = a*c/2 (3.1)

С другой стороны (см. Полезные формулы расчета, Формула расчета радиуса вписанной окружности):
S = r*p, где
r — радиус вписанной окружности, r = (a+c-b)/2.
p — полупериметр.

Таким образом:
S = r*p = (a+b+c)/2 * (a+c-b)/2 =
  = (a2+2*a*c+c2-b2)/4

С учетом (3.1):
a*c/2 = (a2+2*a*c+c2-b2)/4

Приводя к общему знаменателю и пренося в левую часть, получим:
a2+c2-b2 = 0, или
a2+c2 = b2

4. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача -- пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.