Формулы треугольника. Площадь треугольника, прямоугольный треугольник, теорема Пифагора, радиус вписанной окружности, радиус описанной окружности.

Треугольник обладает замечательным свойством — это жесткая фигура, т.е. при постоянной длине сторон нельзя изменить форму треугольника. Это свойство треугольника делает его незаменимым в технике и строительстве. Элементы конструкции в форме треугольника сохраняют свою форму, в отличие, например, от элементов в форме квадрата или параллелограмма. Кроме того, треугольник является простейшим многоугольником и любой многоугольник можно представить в виде набора треугольников.

Основные свойства и формулы треугольника

Обозначения:
A, B, C — углы треугольника,
a, b, c — противолежащие стороны,
R — радиус описанной окружности,
r — радиус вписанной окружности,
p — полупериметр, (a + b + c) / 2,
S — площадь треугольника.


Стороны треугольника связаны следующими неравенствами
a ≤ b + c
b ≤ a + c
c ≤ a + b
В случае выполнения равенства в одном из них треугольник называется вырожденным. Далее везде предполагается невырожденный случай.

Треугольник можно однозначно (с точностью до сдвига и поворота) определить по следующим тройкам основных элементов:
a, b, c — по трем сторонам;
a, b, C — по двум сторонам и углу между ними;
a, B, C — по стороне и двум прилежащим к ней углам.

Сумма углов любого треугольника постоянна
A + B + C = 180°

1. Прямоугольный треугольник. Определение тригонометрических функций.

Рассмотрим прямоугольный треугольник, показанный на рисунке.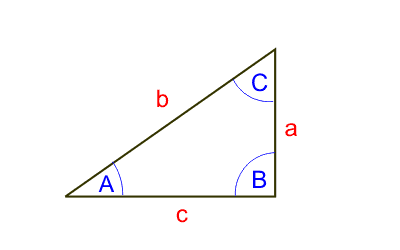
Угол B = 90° (прямой).
Функция синус:sin(A) = a/b.
Функция косинус:cos(A) = c/b.
Функция тангенс:tg(A) = a/c.
Функция котангенс:ctg(A) = c/a.

2. Прямоугольный треугольник. Тригонометрические формулы.

a = b * sin(A)
c = b * cos(A)
a = c * tg(A)

См. также:

• Теорема Пифагора — несколько простых доказательств теоремы.
• Тригонометрические функции

3. Прямоугольный треугольник. Теорема Пифагора.

b2 = a2 + c2
С помощью теоремы Пифагора можно построить прямой угол, если под рукой нет подходящих инструментов, например, угольника. С помощью двух линеек или двух кусков веревки отмеряем катеты длиной 3 и 4. Потом сдвигаем или раздвигаем их, пока длина гипотенузы не станет равной 5 (3² + 4² = 5²).

На станице Теорема Пифагора приведено несколько простых доказательств теоремы.

4. Теорема синусов

a/sin(A) = b/sin(B) = c/sin(C) = 2*R

5. Теорема косинусов

Cos(A) = (b2+c2-a2)/(2*b*c)

6. Формула расчета площади треугольника (1)

S = b*c*sin(A)/2

7. Формула расчета площади треугольника (2). Формула Герона

S = (p * (p-a) * (p-b) * (p-c))1/2

8. Формула расчета площади треугольника (3)

S = p * (p-a) * tg (A/2)

См. также:

• Формулы площади

9. Формула расчета радиуса описанной окружности (1)

R = a/(2*sin(A))

10. Формула расчета радиуса описанной окружности (2)

R= a*b*c /(4*S )

11. Формула расчета радиуса вписанной окружности (1)

R = S/p

12. Формула расчета радиуса вписанной окружности (2)

R = (p-a)*tg(A/2)